it is acknowledged that it is downloaded from the site below http://blog.plover.com/math/sqrt-2-new.html
A new proof that the square root of 2 is irrational
The proof was discovered by Tom M. Apostol, and was published as "Irrationality of the Square Root of Two - A Geometric Proof" in the American Mathematical Monthly, November 2000, pp. 841–842.
In short, if √2 were rational, we could construct an isosceles right triangle with integer sides. Given one such triangle, it is possible to construct another that is smaller. Repeating the construction, we could construct arbitrarily small integer triangles. But this is impossible since there is a lower limit on how small a triangle can be and still have integer sides. Therefore no such triangle could exist in the first place, and √2 is irrational.In hideous detail: Suppose that √2 is rational. Then by scaling up the isosceles right triangle with sides 1, 1, and √2 appropriately, we obtain the smallest possible isosceles right triangle whose sides are all integers. (If √2 = a/b, where a/b is in lowest terms, then the desired triangle has legs with length b and hypotenuse a.) This is ΔOAB in the diagram below:
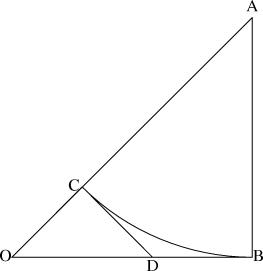
Now construct arc BC, whose center is at A. AC and AB are radii of the same circle, so AC = AB, and thus AC is an integer. Since OC = OA - CA, OC is also an integer. Let CD be the perpendicular to OA at point C. Then ΔOCD is also an isosceles right triangle, so OC = CD, and CD is an integer. CD and BD are tangents to the same arc from the same point D, so CD = BD, and BD is an integer. Since OB and BD are both integers, so is OD.Since OC, CD, and OD are all integers, ΔOCD is another isosceles right triangle with integer sides, which contradicts the assumption that OAB was the smallest such.The thing I find amazing about this proof is not just how simple it is, but how strongly geometric. The Greeks proved that √2 was irrational a long time ago, with an argument that was essentially arithmetical. The Greeks being who they were, their essentially arithmetical argument was phrased in terms of geometry, with all the numbers and arithmetic represented by operations on line segments. The Tom Apostol proof is much more in the style of the Greeks than is the one that the Greeks actually found![ 20070220: There is a short followup to this article. ]